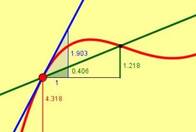
Differenzialrechnung
Die Anwendung der Differenzialrechnung in der Naturwissenschaft, der Technik und der Wirtschaft ist kaum mehr wegzudenken. Der große Erfolg dieser Rechenmethode führt zu neuen Erkenntnissen und Fortschritten. Es soll hier hauptsächlich auf die zentralen Begriffsbildungen eingegangen werden
-
Geschichte der Infinitesimalrechnung
Untrennbar mit der Differenzialrechnung ist auch die Integralrechnung (zusammen die Infinitesimalrechnung) zu erwähnen. Es werden hier die historischen Wegbereiter und die eigentlichen Protagonisteten, Leibniz und Newton, angeführt. Weiters wird auf die moderne Weiterenwicklung verwiesen. Detailansicht
-
Lehrgang Differenzialrechnung
Dieser Lehrgang zum Selbststudium ist, gut strukturiert, in 3 Teilen aufgebaut. Links führen auch zur Wiederholung der zugehörigen Grundlagen. Multimedial aufgebaut: Videos, interaktive Seiten, Formelsammlungen u.v.m Detailansicht
-
Differenzialrechnung
Der Begriff des Differenzialquotienten wird in diesem youtube-Video anschaulich erklärt. Detailansicht
-
-
Differenzenquotient - Differenzialquotient
Auflistung vieler Beispiele, wie man auf verschiedene Arten den Differenzenquotient erhalten kann und damit den Differenzialquotienten daraus ermitteln kann. Detailansicht
-
Sekanten/Tangentensteigung - Ableitungsfunktion
Dieses dynamische Geogebra-Arbeitsblatt geht von einer beliebigen Funktion aus. Mittels Ziehen eines Kurvenpunktes kann man alle Tangenten darstellen. An einer festen Stelle werden durch einen Schieberegler Näherungssekanten erzeugen. Für Einsatz auf allen Abstraktionsstufen gut geeignet! Detailansicht
-
Änderungsrate 1
Es werden hier verschiedene Aspekte dieses Begriffes zusammengefasst. Detailansicht
-
Änderungsrate 2
Kompakte und einfache Erklärung des Begriffes mittlere bzw. momentane Änderungsrate. Als Zusammenfassung bzw. Wiederholung gut geeignet. Detailansicht
-
Änderungsrate 3
Bewährte Videopräsentation des Änderungsraten-Begriffes. Längere und in die Tiefe gehende Ausführung. Detailansicht
-
Anwendungen in der Differenzialrechnung 1
Anwendungen v.a. innerhalb der Mathematik, sehr umfassend! Detailansicht
-
Anwendungen in der Differenzialrechnung 2
Anwendungsaufgaben für den Einsatz im Unterricht von Bundesarge angewandte Mathematik Detailansicht
-
Anwendungen in der Differenzialrechnung 3
Aufgaben für den Unterricht: Übungen zu den zentralen Begriffen und Anwendungen in der Physik und Technik Detailansicht